Graphs and Graph Applications

In this post, we will introduce basic concepts of graphs, and some typical applications of graph algorithms.

What is Graph

All things in the universe, from stars and planets as large as they are, to atoms and molecules as small as they are, exist in connections with each other. Graph is the most natural and suitable data structure for describing the relationships between these individual entities. A graph consists of a series of vertices (i.e., individuals) and edges (i.e., relationships between individuals), and both vertices and edges can be accompanied by some description of their own features.

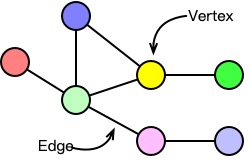
The graph data commonly seen in our daily life includes social networks, transportation networks, and biological structure. For example, in social networks, each user can be regarded as a vertex in the graph, and the interactive relationship between users can be regarded as an edge. For instance, WeChat’s social network can be seen as a graph composed of vertices (individuals, official accounts) and edges (follow, like). For a city’s transportation network, we can regard each subway station as a vertex and the lines connecting various subway stations as edges. In the biological structure, each protein can be regarded as a vertex, and the interaction between proteins can be regarded as edges.

Algorithms and Applications of Graph Computation

Broadly speaking, all analytical calculations based on graph data belong to graph computation, making its application areas very extensive. Considering that graph data can describe the relationships between individual entities, graph computation is particularly suitable for analyzing and computing big data related to correlation relationships. The core of graph computation lies in graph algorithms. In the following, we will classify and introduce some commonly used graph algorithms through a few simple examples.

Graph Analysis Algorithms

Graph analysis algorithms analyze and mine the overall characteristics of the whole graph or the local characteristics of partial graph structures by iteratively traversing vertices or edges in graph data. Let’s take path planning as an example to illustrate graph analysis algorithms. Suppose you ordered takeout from a restaurant located at address B while you are at home at address A. How does the delivery man find the optimal delivery route from B to A and deliver the takeout to you as quickly as possible? If we regard every address in the city as a vertex, the road connecting two addresses as an edge, and the length of the road as the feature of the edge, we can transform this problem into finding the shortest path from B to A. To solve this problem, we can use the classic Dijkstra algorithm.

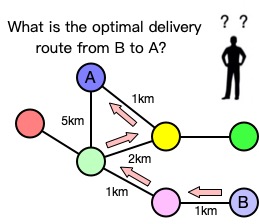
In addition to the shortest path algorithm, commonly used graph analysis algorithms also include PageRank (analyzing the importance of vertices in the graph), Breadth-First Search (BFS) (traversing vertices in the graph according to certain rules), and Connected Components (calculating sets of vertices connected to each other in the graph). As shown in the above examples, graph analysis algorithms are based on graph theory and use relationships between vertices to infer the overall or local structural characteristics of complex graph data. We can use these algorithms to discover hidden information and solve practical business problems. For example, search engines can use the PageRank algorithm to rank the weight of web pages and show the most important web pages to users first.

Community Detection Algorithms

“Community” phenomena often exist in graph data, with each community consisting of a group of vertices. For a community, the relationships (edges) between internal vertices are far more than those between external vertices of the community. Community detection algorithms help to discover group behaviors or preferences within communities, find nested relationships, and are often applied to the visualization of graph data.

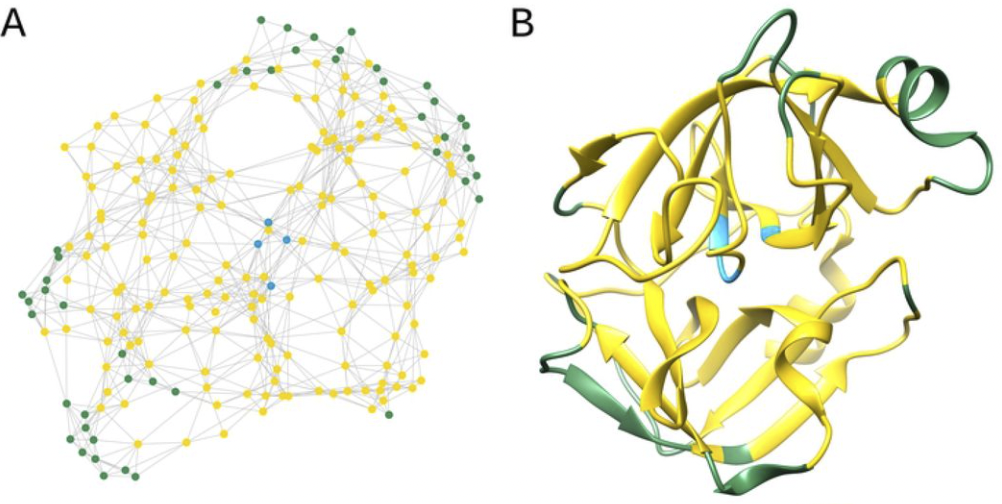
Let’s take the analysis of protein function as an example to introduce community detection algorithms. We can regard each protein as a vertex in the graph, and the interaction between proteins as edges, thus forming a protein interaction graph as shown in the figure below. In biology, proteins need to work closely together to complete a specific physiological function. Through community analysis algorithms, we can obtain several communities (proteins in different communities have different colors), and each community of proteins can be considered to cooperate with each other to complete a specific function.

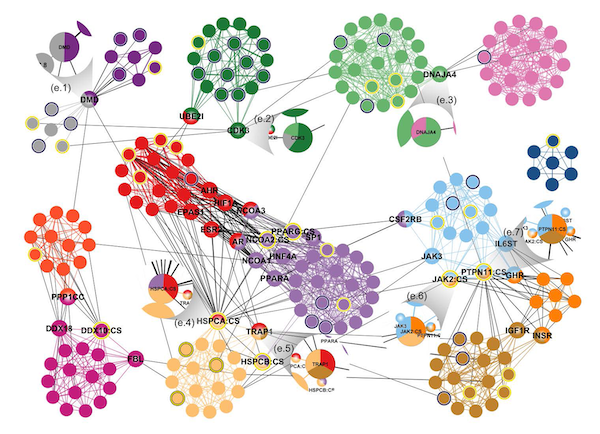
Pattern Matching Algorithms

Another field in which graph computing can demonstrate its capabilities is pattern matching algorithms. Graph pattern matching aims to find a series of subgraph structures that meet the given pattern, which has been widely used in various business scenarios. Taking financial transactions as an example, the flow of funds between accounts makes graph data a suitable data structure for representing financial transaction data. In the financial industry, one important type of anomalous transaction that needs to be detected is credit card cash-out, where the funds from a credit card flow through one or more intermediate transactions before returning to the account holder’s account. As shown in the figure below, if we represent the transaction relationship between accounts as a graph structure, this problem can be transformed into finding the “cycle” (starting from a vertex and following the edges can return to this vertex) in the graph.

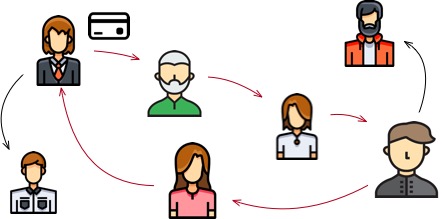
According to the different structural patterns of the queries, pattern matching algorithms can be divided into the following categories: vertex queries (such as reachability queries, neighbor node queries, etc.), path queries (such as a path satisfying specific conditions), and subgraph structure queries (such as subgraph isomorphism). Pattern matching algorithms are widely used, apart from the financial transaction field, they also play an important role in anomaly event detection in social media and hacker activity detection in computer networks.

Recommendation Algorithms

There is significant commercial value in using social networks to recommend products that users are most interested in. Currently, collaborative filtering algorithms are the most widely used algorithm in recommendation systems, and graph computing can also enhance collaborative filtering algorithms. For example, if two users are friends and live in the same location, and one user visits a restaurant and likes it, the recommendation algorithm will assume that the other user is also likely to be interested in this restaurant and push the information of the restaurant to her. By constructing a graph structure as shown in the figure below, we can naturally solve these problems on the graph.

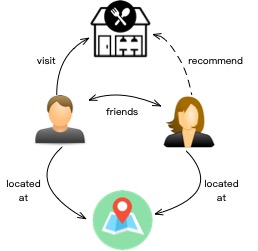
Structure Prediction Algorithms

Due to the existence of noise in graph data, there are often partial errors in the vertices and edges of the graph, which requires the use of graph structure prediction algorithms to correct the graph data. As shown in the figure below, in a social network, users A and B have many mutual friends, but there is no edge between A and B. Graph structure prediction algorithms often assume that two people with many mutual friends are likely to be friends, so they believe that there should be an edge between A and B.

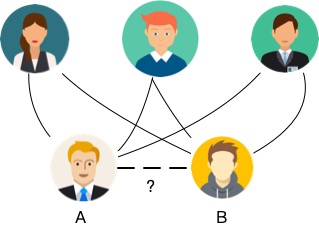
Traditional graph structure prediction algorithms usually use static indicators such as the number of mutual friends, Katz centrality, and Adamic-Adar to correct the graph structure. In recent years, with the rapid development of deep learning technology, graph neural networks have become another popular class of graph structure prediction algorithms. Graph neural networks use neural networks to automatically mine features that are closely related to graph structure prediction, which greatly reduces the degree of human involvement and achieves better results compared to traditional methods.

Summary

The core of graph computing is how to model data as a graph structure and how to transform the solution of a problem into a computational problem on the graph structure. When the problem involves relational analysis, graph computing can often naturally represent the solution process as a series of operations and computations on the graph structure. However, the problems that graph computing needs to solve are diverse, and it is difficult to use one set of computation models to solve all problems. We will introduce in detail the classification of graph computing, as well as the characteristics and key technologies of each type of graph computing in later articles.