Categories, Languages, and Systems of Graph Computing

In this post, we will introduce the categories, languages, and systems of graph computing.

What is Graph Computing

In real life, many types of data can be modeled as a graph, which is an abstract structure. This efficient and compact data format can represent rich information such as topology, attributes, and timing. The goal of graph computing is to mine valuable knowledge or patterns from the graph structure, such as frequent patterns and causal relationships. With the advent of the information age, there is an explosive growth in data volume, which has created a demand for efficient processing of large-scale graph data. Graph computing has become a hot topic in both industry and academia, leading to the development of various graph computing systems and optimization research.

Due to complex business scenarios, there are various types of graph computing. Currently, there are three main categories of graph computing: graph interactive queries, graph analysis, and graph learning.

Graph Interactive Queries

The graph data is typically vast, and graph interactive queries often focus on a relatively limited number of vertices and edges that satisfy specific criteria. These vertices and edges create specific paths or subgraph patterns, as illustrated in the image below. For example, finding the optimal route from one location to another or logistics path information are typical path query scenarios. Subgraph patterns are another form of graph query where a particular pattern is represented with a subgraph, and matching queries are performed on this subgraph within the entire graph.

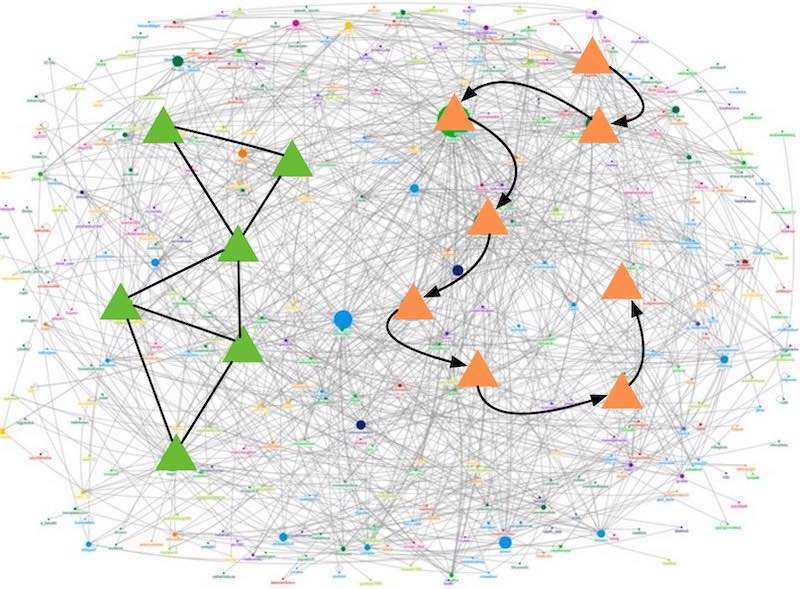
The essence of a path query is graph traversal, which generally involves the following steps: first, set specific vertices in the graph to be queried; then, each vertex to be queried finds the target vertex set via its connected edges that meet the criteria, checks whether the target vertices meet the query result, and if so, adds the target to the result set; otherwise, sets the target vertex as a new vertex to be queried. This process is repeated until there are no more vertices to be queried. In summary, during the entire graph query process, the graph is traversed step by step according to the user-specified criteria, and the desired results are obtained in the end.

Another type of graph query is the subgraph query, which is based on the theoretical foundation of subgraph isomorphism. Users provide the subgraph to be queried (vertices, edges, and the criteria they need to satisfy), and then search for all results that meet the criteria on the data graph. Each result is a subgraph in the data graph that is isomorphic to the query graph, and the vertices and edges mapped by the subgraph satisfy the corresponding criteria on the query graph. In summary, the aim is to search for a specific structure that the user cares about in the large graph.

The two most common languages for graph queries are Gremlin and Cypher. Gremlin is based on Groovy, but there are many language variations available for developers to write queries using native programming languages such as Java and Python. It incorporates both imperative and declarative semantics, making it easy to express graph traversal logic. As a result, it has been adopted by numerous graph database systems, including JanusGraph, InfiniteGraph, Cosmos DB, DataStax Enterprise (5.0+), and Amazon Neptune. On the other hand, Cypher is a graph query language that employs pattern matching based on description. Due to its similarity to SQL, it has the advantage of simple syntax and high flexibility. This feature has led to its adoption by systems such as neo4j, RedisGraph, and AgensGraph.

For instance, if we consider a graph with nodes representing people and locations, the query statements for finding people who live with Mike in both Gremlin and Cypher are shown below.

Gremlin:

g.V().has('name', 'mike').as('a')
.out('lives').in('lives').where(neq('a'))
.values('name')

Cypher:

MATCH
(src:person{name:"mike"})-[:lives]->()<-[:lives]-(dst:person)
RETURN dst.name

When it comes to processing data, graph querying has distinct computational features. Its characteristics of massive data and poor locality require the system to optimize various aspects such as distributed task partitioning, load balancing, and communication scheduling. The high computational complexity and low latency requirements of users make the system’s concurrency particularly crucial. The presence of super nodes, causing memory inflation, and limited memory in interactive environments pose significant challenges to memory management in the system.

Graph Analysis

Graph querying involves accessing a limited number of vertices or edges that satisfy specific conditions and returning results in real-time. For example, walking two steps from a particular vertex based on specific conditions and returning the paths that meet the criteria. In contrast, graph analysis involves more complex calculations, focusing on analyzing and mining the overall characteristics of the entire graph or the associated information between entities. This includes clustering all vertices in the graph according to certain rules.

Graph theory is a traditional branch of mathematics that has been studied for hundreds of years, resulting in numerous algorithms related to graph analysis. These range from classical algorithms like shortest path and connected component to practical problems in artificial intelligence such as community discovery, collaborative filtering, and pattern mining. As a result, graph analysis has been applied in an increasing number of scenarios, and large-scale graph analysis has become a research hotspot. According to GraphX, common categories of graph analysis algorithms include:

• Simple graph analysis algorithms
  • PageRank
  • Shortest path
  • Graph coloring
  • Connected component
• Community discovery algorithms
  • Triangle counting
  • K-core decomposition
  • K-Truss
• Pattern matching algorithms
  • Graph simulation
  • (Sub)graph isomorphism
  • Keyword search
• Collaborative filtering algorithms
  • Alternating least squares (ALS)
  • Stochastic gradient descent (SGD)
  • Tensor Factorization
• Structural prediction algorithms
  • Loopy belief propagation
  • Max-product linear programs
  • Gibbs sampling

In 2010, Google publicly released the Pregel system, marking the first distributed system specifically designed for analyzing large-scale graph data. The system was based on a vertex-centric programming model and sparked a series of subsequent academic research and open-source systems. The programming model used a local, vertex-oriented computing approach, encouraging users to “think like a vertex”. This model has natural scalability and parallelism, making it widely used. Systems that follow this model optimize it from various aspects such as programming interfaces, task partitioning, and execution mechanisms, such as the classic programming model GAS of PowerGraph.

Another type of system adopts more advanced programming models, such as Giraph++, which first proposed using subgraphs as the basic unit of computation, achieving higher execution efficiency. The PIE model proposed by GRAPE can automatically parallelize single-machine graph algorithms, greatly reducing the programming difficulty for users while achieving high performance.

Designing graph analysis systems is a challenging process due to the complexity of graph data. Considerations such as how to effectively utilize underlying hardware resources, how to partition and maintain distributed consistency, how to implement more efficient execution modes and task scheduling strategies, how to develop advanced computing and programming models, and how to create better system fault tolerance mechanisms must all be taken into account.

Graph Learning

Graph learning, also known as graph-based machine learning, aims to integrate the structural information of graphs into machine learning models. With the widespread application of artificial intelligence technologies, represented by deep learning, and the stronger expressive power of graph structures, graph learning has become a hot topic and has led to breakthrough progress in causality and interpretability. Graph learning has been applied in various fields, such as search and recommendation, advertising, financial risk control, intelligent transportation, medical care, and cities. However, graph learning also faces new technical challenges, such as large-scale data, heterogeneity of vertices and edges, multimodal attribute features, and dynamic changes in structure or attributes over time.

The traditional approach to graph learning is graph embedding. Graph embedding represents each vertex in the graph as a low-dimensional vector, retaining as much structural and content information of the graph as possible. This representation vector can be used as a feature for subsequent learning tasks such as link prediction and vertex classification. The figure below shows a classic example, where the left side is the original graph structure, and the right side is a mapping scheme obtained by representation learning. The mapping scheme transforms each vertex in graph A into a point in a two-dimensional coordinate system, that is, a two-dimensional vector. In the coordinate space obtained by the mapping, the closely connected vertices in the original graph (i.e., vertices of the same color) remain close to each other.

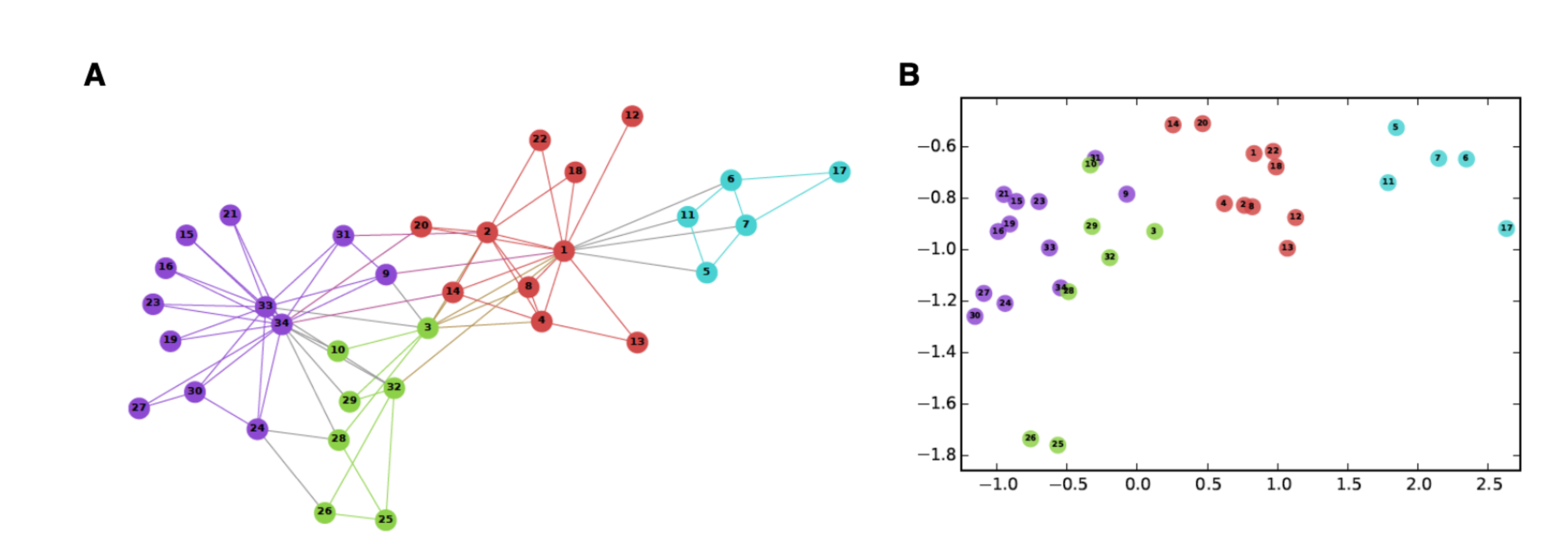
Significant amount of research has been devoted to graph embedding, leading to various solutions for different types of data, such as isomorphic graphs, heterogeneous graphs, attribute graphs, and dynamic graphs. Classic algorithms such as DeepWalk, LINE, and Node2Vec propose different approaches to generate data based on random walks, followed by parameter optimization through training to generate a probabilistic model.

Another crucial type of graph learning is graph neural networks (GNNs). Traditional neural networks are limited to solving problems in Euclidean space, where data is complete, neat, and regular. For example, in a photo, each pixel is fixedly adjacent to eight vertices, enabling each vertex to correspond to a vector of the same length containing its own information and neighbor information. However, GNN extends classic neural network models like Recurrent Neural Networks (RNNs) and Convolutional Neural Networks (CNNs) to graphs, allowing it to solve problems in non-Euclidean space. This is because the graph structure is irregular, where the number of neighbors of each vertex is different, leading to local dimensions of variable length. Unlike graph embedding, where the focus is on learning the embedding of each vertex, the primary purpose of GNN is to learn the aggregation function, allowing all vertices to calculate their embedding using the same function based on local information. Even if the graph structure changes or a new graph is encountered, meaningful results can still be calculated using the original function. Several classic algorithms for GNN exist, and readers can refer to relevant literature to learn more.

In summary, both graph embedding and GNNs are essential types of graph learning that play different roles in integrating the structural information of graphs into machine learning models. They have made significant contributions to causality, interpretability, and have been applied in various fields. However, as graph datasets become more complex and diverse, it is crucial to continue developing new techniques and algorithms to address these challenges.

Conclusion

Due to the strong dependency, poor locality, irregular distribution, and diverse structures of graph data, traditional parallel systems for big data are difficult to apply. In addition, different types of computational features and paradigms also bring diversified requirements for the design of graph computing systems.

An ideal graph computing system should be versatile, high-performance, and easy to use. In terms of versatility, we hope that it supports multiple types of computations such as graph interactive queries, graph analysis, and graph learning, and compatible with language standards and the industry ecology. In terms of performance, it should support low-latency interactive queries, have high-performance graph analysis capabilities, provide large-scale graph storage, and achieve high scalability. In terms of ease of use, it should provide a unified programming model, highly abstracted, simple and flexible language, and implement simple system deployment, easy cluster management, and provide a visual interface.

To meet the various challenges faced by graph computing systems, meet the needs of real-world application scenarios, and provide one-stop efficient solutions, is the original intention of the GraphScope design. The GraphScope system proposes multiple innovative technologies and is continuously iterating rapidly. It has proved to achieve significant new business value in multiple key internet fields such as risk control, e-commerce recommendation, advertising, network security, knowledge graph, and is committed to empowering more important application scenarios.