Processing 100-billion edges in one second: Empowering Graphalytics with GPU Acceleration
 Graph algorithms serve as essential building blocks for a wide range of applications, such as social network analytics, routing, constructing protein network and De Bruijn graphs, and mining valuable information in RDF (Resource Description Framework) graphs. Generally, graph analytics involve propagating labels across edges or iteratively accumulating values from adjacent vertices. Existing engines in both academia and industry, like PowerGraph, Pregel, and GraphX, have paved the way. However, in the era of big data, the computational and storage complexity of sophisticated algorithms coupled with rapidly growing datasets have exhausted the limits of a single device.
Graph algorithms serve as essential building blocks for a wide range of applications, such as social network analytics, routing, constructing protein network and De Bruijn graphs, and mining valuable information in RDF (Resource Description Framework) graphs. Generally, graph analytics involve propagating labels across edges or iteratively accumulating values from adjacent vertices. Existing engines in both academia and industry, like PowerGraph, Pregel, and GraphX, have paved the way. However, in the era of big data, the computational and storage complexity of sophisticated algorithms coupled with rapidly growing datasets have exhausted the limits of a single device.
Traditionally, graph analysis tasks, characterized by data-intensive workloads, have been performed on CPUs. However, the emergence of diverse new hardware in recent years has led to the recognition of the potential in constructing heterogeneous computing platforms using accelerator cards (such as FPGAs and GPUs). These accelerators often offer higher degrees of parallelism; for instance, an Nvidia V100 GPU can provide over 5,000 computation cores. Additionally, they exhibit enhanced memory bandwidth capabilities; HBM, for instance, can deliver several TB/s of memory bandwidth. Numerous tasks have already harnessed the potential of such accelerator to achieve significant performance boosts, including deep learning and image processing, and graph computation is no exception.
CPU vs GPU
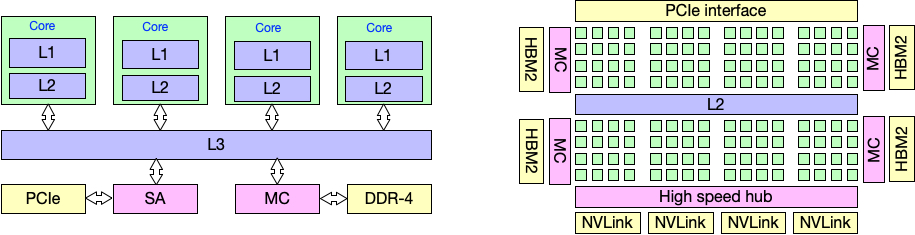
The above figure illustrates the key differences in architecture between CPUs and GPUs. CPUs feature relatively complex components, with most of the area dedicated to elements like prefetching, branch prediction, and caching, all aimed at improving CPU core computational efficiency, enabling them to handle intricate logic. In contrast, GPUs have simpler components but stack a large number of cores, with longer pipelines. When processing data, GPUs operate in a SIMT (Single Instruction, Multiple Threads) manner, typically grouping 32 threads together (some GPUs use groups of 64 threads), known as thread warps (warp in Nvidia GPUs, wave in AMD GPUs). These thread warps execute the same instruction stream simultaneously, and GPUs rely on warp schedulers to hide data fetch latencies. Moreover, GPUs have multiple memory hierarchies, necessitating data movement between main memory, video memory, on-chip shared memory, and vector registers.
| E5 2682 | NVIDIA V100 | |
|---|---|---|
| Clock | 2.5GHz | 877MHz |
| Cores | 8x2 | 5120 (FP32) |
| Prices | ~$1,000 | ~$10,000 |
| Mem b/w | ~40GB/s | ~1TB/s |
| Mem size | ~2TB | 16GB |
This table provides a comparison of specific hardware parameters between CPUs and GPUs. In terms of computational power, GPUs have more cores, allowing them to process more data simultaneously and achieve higher levels of parallelism. This higher parallelism aligns well with the inherently high concurrency of graph algorithms, where each vertex can serve as a parallel unit. Consequently, GPUs demonstrate higher throughput when handling graph algorithms. However, individual GPU cores are weaker and operate at lower clock frequencies compared to CPUs. This characteristic makes GPUs more susceptible to long tail effects when facing load imbalances. In scenarios with imbalanced workloads, most GPU cores might idle while waiting for a few weaker cores to complete their computations. Unfortunately, graph data exhibits inherent irregularity, with skewed edge distributions, where a small number of vertices possess the majority of edges, while most vertices are only connected by a few edges. This irregularity further amplifies the challenge of achieving load balance on GPUs.
When it comes to memory access capabilities, GPUs indeed have higher bandwidth, such as the Nvidia V100 equipped with HBM2, which offers a bandwidth of up to 1TB/s. When GPU warps access adjacent data blocks, they can trigger coalesced memory access, combining multiple memory requests into a single one, providing an advantage over CPUs when handling large amounts of data. However, graph algorithms, especially parallel graph traversal algorithms, require simultaneous processing of a large number of edge data. Although GPUs boast higher memory bandwidth than CPUs, the memory access patterns of graph algorithms are unpredictable. Graph algorithms often need to randomly access a significant amount of data from memory, with each access touching only a small portion of memory (usually representing vertex states, which are not very large in graph analysis tasks). This leads to highly inefficient memory bandwidth utilization, often falling short of the theoretical peak. Additionally, GPU memory capacity is much smaller than that of CPUs, making it challenging for GPUs to handle larger-scale graph data. Furthermore, GPUs struggle to execute algorithms with high memory requirements, especially those that need to store large amounts of intermediate results for graph mining tasks.
When Efficient Graph Algorithms Go Inefficient on GPUs
There is a significant gap between GPU and CPU architectures. Merely transferring CPU algorithms to GPUs may not lead to improved performance; it could even result in performance degradation.
Due to GPUs having more but weaker cores compared to CPUs, graph algorithms running on GPUs should be adjusted appropriately to fully leverage the high concurrency of GPUs. We can achieve higher concurrency by sacrificing some single-thread efficiency in the algorithm. For instance, in the case of the shortest path problem, efficient algorithms like Dijkstra are commonly used on CPUs. Dijkstra maintains a small min-heap and processes only the closest unprocessed vertices to the source vertex, ensuring that each vertex is processed only once. This ordered update approach is highly efficient but limits concurrency based on the degree of each vertex.
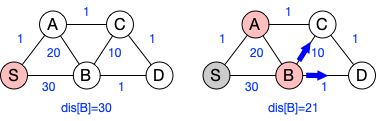
In contrast, Bellman-Ford processes all edges in each update round, providing higher concurrency, but with slightly lower update efficiency as each vertex might be processed multiple times. As shown in the above Figure, during the first round of updates from the source vertex S, vertices A and B are modified, and B’s distance is updated to 30. Subsequently, vertex B updates its neighbors, and in the next round, its distance is modified to 21 via vertex A, triggering updates to other vertices by vertex B. Using Dijkstra, however, only the closer vertices are processed, avoiding repetitive transmission of invalid data by vertex B.
By carefully considering the trade-off between concurrency and single-thread efficiency, graph algorithms can be tailored to effectively harness the potential of GPU’s high concurrency while optimizing their performance on GPUs.
When considering GPUs, a delicate balance between parallelism and computational efficiency must be struck. On one hand, GPUs possess numerous cores; however, utilizing Dijkstra’s algorithm on them demands maintaining a costly concurrent heap, which subsequently curtails the achievable level of concurrency, thus impeding the exploitation of the GPU’s potential. On the other hand, given the relatively weaker nature of GPU cores, adopting algorithms with lower computational efficiency could potentially lead to slower performance compared to directly employing efficient algorithms on CPUs.
To navigate this trade-off, we introduce the concept of an update window, denoted as w.
w serve as a soft adjustable threshold value to balance the efficiency and parallelism.
In each iteration round, only vertices with distances falling within the update window are processed (specifically, those vertices u satisfying dis[u] < w).
After completing updates within a window, the window w is slid, targeting vertices with distances in next window, i.e. interval [w, 2w).
This process continues until all active vertices have undergone updates, signaling the transition to the next iteration.
The size of the window w serves as a tuning parameter, affording users the flexibility to specify w and thus adapt to diverse datasets and computing platforms with precision.
Load Balance is More Important than You Think
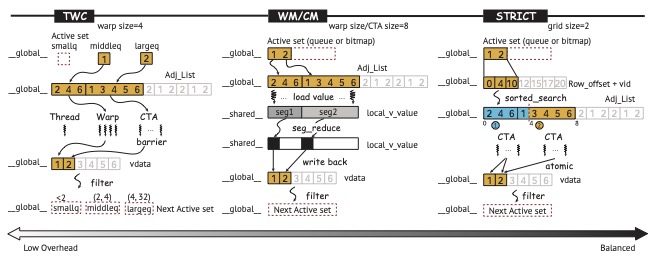
As mentioned above, due to the irregular nature of graph algorithms, which does not align well with the SIMT architecture of GPUs, this irregular computation can result in severe load imbalance, making it crucial for GPU-based graph algorithms. To cope with load imbalance, we have four different load balancing strategies, as illustrated in above.
-
TWC (Thread-Warp-CTA) is the lowest-overhead load balancing method. It divides the currently active vertex set based on their out-degrees into low, medium, and high-degree vertices, and then maps them to threads, warps, and CTAs for processing.
-
WM (Warp-Managed) primarily addresses load imbalance within a warp. It processes a fixed number of vertices as a batch and loads their neighbors into the GPU’s shared memory until all neighbors are processed before moving to the next batch. Each thread performs a binary search on the edges to determine their corresponding vertex.
-
CM (CTA-Managed) is similar to WM, but focuses on load imbalance within a CTA. Like WM, it processes a fixed number of vertices as a batch and loads their neighbors into shared memory. However, CM uses a broader binary search to find the corresponding vertex for the edge, and threads in CM require explicit synchronization.
-
STRICT is the highest-overhead load balancing method, ensuring that each thread in the GPU handles the same number of edges. It enforces equal edge distribution in each CTA, requiring additional preprocessing to partition the edges that need processing, with some nodes’ edges distributed across different CTAs, necessitating atomic operations during updates for consistency.
Theoretically, STRICT guarantees the best load balancing, but it incurs the highest overhead. It is often the optimal choice when the active vertex set contains a vertex with a large number of edges. TWC offers the lowest overhead but only guarantees approximate balance. WM/CM falls between the two extremes, with WM’s primary overhead being the binary search, taking no more than log2(warpsize) steps to complete, while CM’s overhead is log2(blocksize) steps.
Try GPU-based Graphalytics on GraphScope
If you are looking for an out-of-box GPU-based graphalytics library, come and try GraphScope. Our recent update on graph analytical engine (GAE) of GraphScope introduces a new feature for GPU acceleration and achieves amazing performance on large graphs.
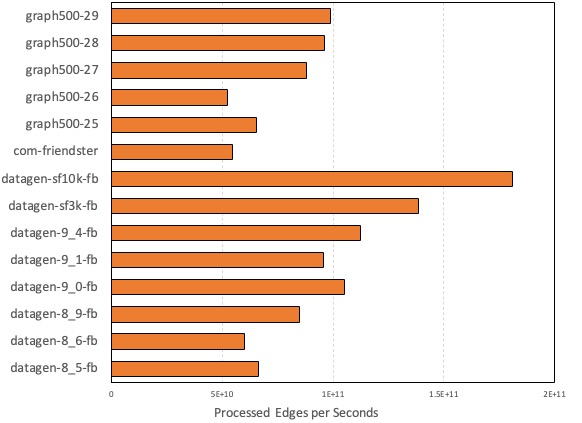
The above chart illustrates the performance achieved by GPU-based GraphScope on a single node with eight A100 GPUs when running on graph data of various sizes. It showcases the throughput in terms of edges processed per second while handling this data. Processing a graph data set with 8 billion edges takes just 85 milliseconds, significantly outperforming the results obtained from a distributed cluster composed of multiple CPU nodes.
GraphScope continues to evolve, and we are working on ways to provide flexibility and performance. We are building out the next version of GraphScope that will start to provide more exciting features like GPU, RDMA and CXL. Reach out to us via Github Discussions. We’re here to help.
References
-
[1] Farzad Khorasani, Keval Vora, Rajiv Gupta, and Laxmi N. Bhuyan. CuSha: vertex-centric graph processing on GPUs. (link)
-
[2] Jianlong Zhong and Bingsheng He. Medusa: Simplified Graph Processing on GPUs. (link)
-
[3] Yangzihao Wang, Yuechao Pan, Andrew Davidson, Yuduo Wu, Carl Yang, Leyuan Wang, Muhammad Osama, Chenshan Yuan, Weitang Liu, Andy T. Riffel, and John D. Owens. Gunrock: GPU Graph Analytics. (link)
-
[4] Tal Ben-Nun, Michael Sutton, Sreepathi Pai, and Keshav Pingali. Groute: An Asynchronous Multi-GPU Programming Model for Irregular Computations. (link)
-
[5] Ke Meng, Jiajia Li, Guangming Tan, and Ninghui Sun. A pattern based algorithmic autotuner for graph processing on GPUs. (link)
-
[6] K. Meng, L. Geng, X. Li, Q. Tao, W. Yu and J. Zhou, “Efficient Multi-GPU Graph Processing with Remote Work Stealing. (link)