GOpt: A Unified Graph Query Optimization Framework in GraphScope
 In this blog, we introduce GOpt, which is a unified graph query optimization framework in GraphScope.
GOpt enables the system to support multiple graph query languages while providing consistent and efficient query optimization. We also present two practical cases to demonstrate the effectiveness of our optimizer.
In this blog, we introduce GOpt, which is a unified graph query optimization framework in GraphScope.
GOpt enables the system to support multiple graph query languages while providing consistent and efficient query optimization. We also present two practical cases to demonstrate the effectiveness of our optimizer.
Background and Challenges
In real applications, there has been a growing interest in integrating graph query semantics with relational query semantics to support more complex queries. A typical querying paradigm, termed as PatRelQuery, involves a two-stage process: first, identifying subgraphs of interest through pattern matching, and subsequently, performing relational operations, such as projection, selection and ordering, on the matched results for further analysis.
Below, we present an example of PatRelQuery, composed using Cypher, which is one of the most widely adopted graph query languages.
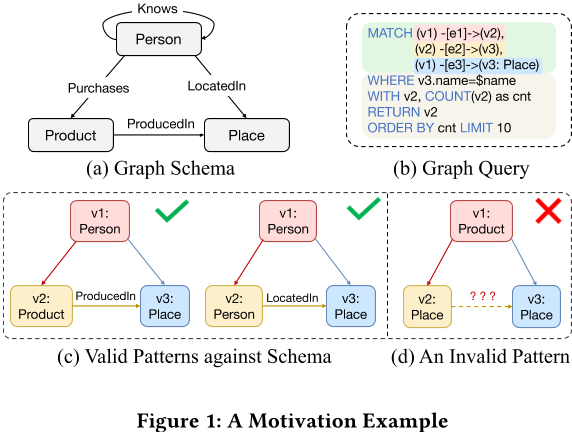
As depicted in Figure 1(a), we consider a graph database comprising vertex types of “Person”, “Product”, and “Place”, alongside edge types of “Purchases”, “LocatedIn”, “ProducedIn”. The PatRelQuery shown in Figure 1(b) begins by identifying a triangle pattern. This pattern imposes a type constraint on vertex $v_3$, designating it as a “Place” as specified in the MATCH clause. Subsequent relational operations are then applied to the results of this pattern match, including filtering based on a specific place name and aggregating the results to return the top 10 entries. These steps are articulated through the WHERE, COUNT, ORDERBY, and LIMIT clauses. Notice that in this query only $v_3$ is explicitly assigned a type constraint, while the other vertices and edges are not. Consequently, these untyped vertices and edges are treated as with arbitrary types. From this example, we distill two primary features for PatRelQuery:
- Hybrid Semantics: PatRelQuery melds graph pattern matching with relational operations, showcasing a high level of expressiveness.
- Arbitrary Types: PatRelQuery allows arbitrary type specification for a greater degree of flexibility in pattern descriptions.
However, such a flexible query representation poses significant challenges for the graph optimizer:
- The optimizer needs to support both graph pattern matching and relational operators within the same framework and perform unified optimization on it.
- The optimizer must identify implicit type constraints within the graph patterns. For instance, in the above example, only the type constraints shown in Figure 1(c) are valid, whereas the combination of type constraints in Figure 1(d) is actually invalid.
To address the above challenges, we propose GOpt, a graph-native optimization framework for PatRelQuery. We summarize the main contributions as follows:
- We have introduced GOpt, which, as far as we know, is the first graph-native optimization framework specifically designed for industrial-scale graph database systems. This framework integrates both graph and relational operations, offering a unified approach to query optimization in complex PatRelQueries across various graph query languages.
- We have designed algorithms for efficient type inference in the context of arbitrary patterns. Our approach also includes a comprehensive set of heuristic optimization rules. Moreover, we have proposed a novel cardinality estimation technique that takes into account the arbitrary types. Building upon this, a cost-based optimizer has been developed, operating within a top-down framework with branch-and-bounding strategies.
- We have implemented GOpt atop the open-source optimization framework Apache Calcite, inheriting its capabilities for optimizing relational operations. This integration has been smoothly executed to include our specialized graph-optimization techniques. The effectiveness of our proposed techniques has been validated through comprehensive experimental evaluations.
System Overview
First, we provide an overview of the system architecture of GOpt, as illustrated in Figure 2.
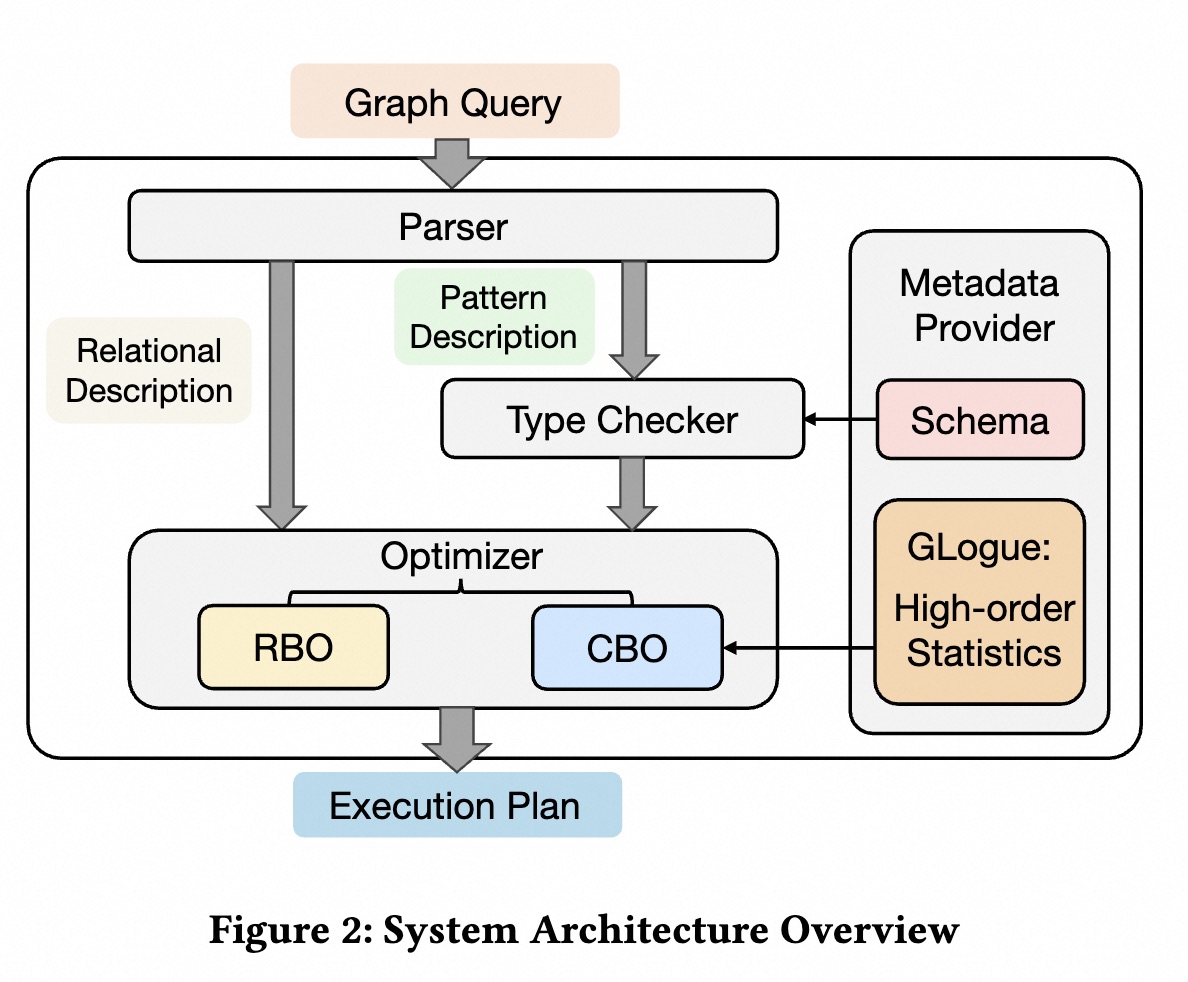
The overall GOpt system is composed of four principal components:
Parser plays a pivotal role in transforming user queries into a language-independent query plan based on a unified intermediate representation (IR). It accommodates various clients for different graph query languages, such as Gremlin and Cypher. The parser enables the decouple of the query language and the query optimization framework, which allows the system to support multiple query languages with the extensive reuse of techniques developed within GOpt.
Type Checker is responsible for inferring and validating the type constraints in the query pattern against the graph schema. We allow users to provide arbitrary type constraints for vertices and edges in their query patterns, and even allow them not to specify any type constraints at all. The type checker is responsible for inferring implicit type constraints within the user’s query based on the graph schema. At the same time, the type checker will also promptly report INVALID errors for queries that are not valid.
Optimizer aims to optimize the logical plan to derive the most efficient physical plan. It employs a combination of Rule-based Optimization (RBO) and Cost-based Optimization (CBO). The RBO consists of a set of rules heuristically applied to the logical plan to produce a more efficient equivalent. The CBO consists of two phases: First, to optimize pattern matching, we devise a top-down search algorithm with branch-and-bounding strategies, to identify the optimal plan for arbitrary pattern. Secondly, to refine the relational part, we integrate the proposed graph optimizer with the optimization framework Apache Calcite, leveraging its advanced optimization capabilities for relational queries.
Metadata Provider consists of two parts: the graph schema which defines the vertex and edge types within the data graph and assists the Type Checker in deducing and affirming type constraints within the query plan, and the statistics provider known as GLogue, which precomputed the frequencies of certain small patterns in the data graph to serve as high-order statistical information and provides this high-order statistics for more accurate cost estimation in the optimization phase.
Query Processing and Optimization
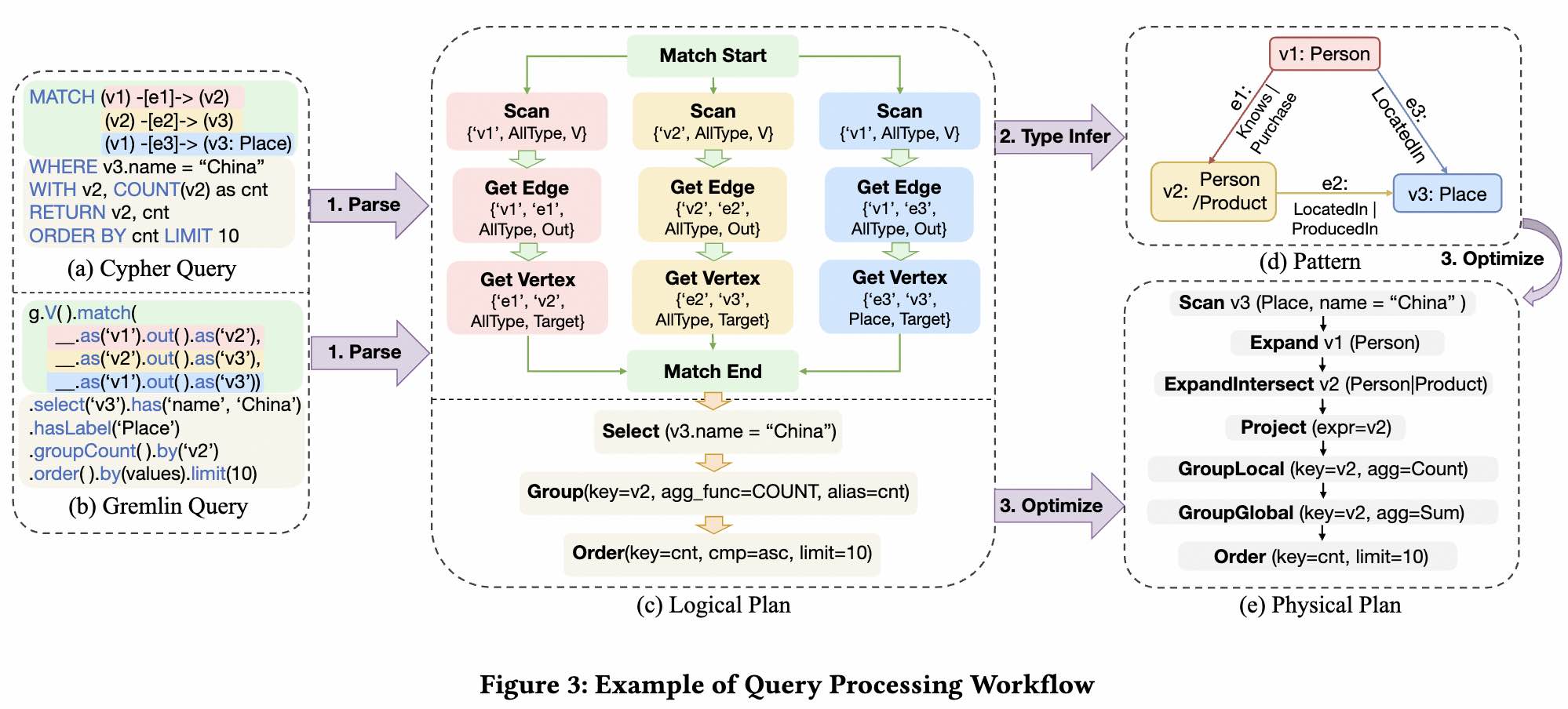
Next, we present the workflow of query processing and optimization within GOpt as depicted in Figure 3, and we will delve into the details in the following.
Query Processing
First, we proposed a unified Intermediate Representation (IR) framework as a foundation to process PatRelQueries. The IR abstraction defines a data model $\mathcal{D}$ that describes the structure of the intermediate results during query execution,and a set of operators $\Omega$. The data model $\mathcal{D}$ presents a schema-like structure in which each data field possesses a name, denoted as a String type, accompanied by a designated datatype. The supported datatypes includes graph-specific datatypes such as Vertex, Edge, and Path, and general datatypes including Primitives and Collections. The operators in $\Omega$ operate on data tuples extracted from $\mathcal{D}$, and produce a new set of data tuples as a result. The set $\Omega$ is composed of graph operators such as GetV, EdgeExpand and PathExpand, and relational operators such as Project, Select, Join, etc.
The IR abstraction enables the opportunity to convert various query languages into a unified form. Currently, GOpt supports two of the most widely used graph query languages, Cypher and Gremlin. We employs the parser tool provided by Antlr to interpret the queries into an Abstract Syntax Tree (AST), based on which we further build a logical DAG that each node corresponds to an operator defined in IR. As shown in Figure 3, the queries written in Cypher and Gremlin respectively can be parsed in to a unified DAG shown in Figure 3(c).
Notice that in the Match part in Figure 3(c), the user has not provided explicit type constraints for vertices $v_1$ and $v_2$. However, based on the graph schema, given that $v_3$ is a “Place”, we can infer that $v_1$ and $v_2$ could be either “Person” Or “Product”. Similarly, considering the edge ($v_1$, $v_2$), the type of $v_1$ can be further refined as “Person”. Through type inference, we can obtain a graph pattern that only includes valid types as shown in Figure 3(d).
Building on the DAG with valid types, we further optimize it to obtain the optimal physical plan shown in Figure 3(e), which is then submitted to the backend for execution. Next, we will introduce the process of query optimization.
Query Optimization
The optimizer within GOpt comprises two parts: Rule-Based Optimization (RBO) and Cost-Based Optimization (CBO). The optimization process is illustrated in Figure 4.
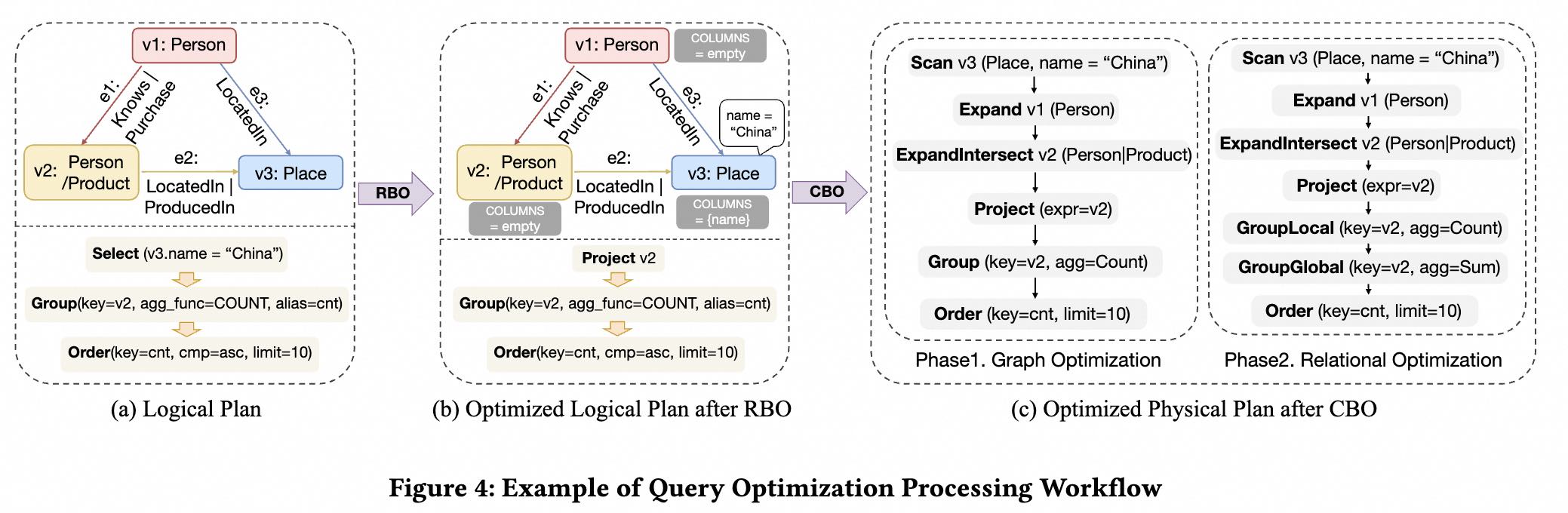 To optimize PatRelQueries, we devised a comprehensive set of rules, taking into account potential optimization opportunities among graph operators, relational operators, and between the two. For example, as shown in Figure 4, since only the name attribute of $v_3$ is needed for filtering, we use the FieldTrimRule (a relational optimization) to eliminate other unnecessary attributes, avoiding the retention of irrelevant data during computation. Besides, pattern matching often requires matching adjacent edges, and then further matching neighboring vertices through those edges. Under certain conditions, this can be optimized by the ExpandGetVFusionRule (a graph operator optimization), which combines the two operations into a direct neighboring vertex match. In this query, we also see that after performing pattern matching, the user further selects results that meet certain conditions through a Select operation. We can apply the FilterIntoMatchRule (a graph-relational operator optimization) to push the filter conditions directly into the graph operators, ensuring that only results that meet the filter conditions are matched during the pattern matching process.
To optimize PatRelQueries, we devised a comprehensive set of rules, taking into account potential optimization opportunities among graph operators, relational operators, and between the two. For example, as shown in Figure 4, since only the name attribute of $v_3$ is needed for filtering, we use the FieldTrimRule (a relational optimization) to eliminate other unnecessary attributes, avoiding the retention of irrelevant data during computation. Besides, pattern matching often requires matching adjacent edges, and then further matching neighboring vertices through those edges. Under certain conditions, this can be optimized by the ExpandGetVFusionRule (a graph operator optimization), which combines the two operations into a direct neighboring vertex match. In this query, we also see that after performing pattern matching, the user further selects results that meet certain conditions through a Select operation. We can apply the FilterIntoMatchRule (a graph-relational operator optimization) to push the filter conditions directly into the graph operators, ensuring that only results that meet the filter conditions are matched during the pattern matching process.
Next, we will demonstrate the cost-based optimization techniques within GOpt, focusing mainly on the optimization of graph patterns, which is often the most crucial part of the optimization process. Drawing from the capabilities provided by our previous work GLogS, we have designed effective graph pattern matching optimization techniques:
- Hybrid implementation strategies for pattern matching. For the physical implementation of graph pattern matching, we consider both the Worst-Case Optimal Join (WCOJ) and the traditional BinaryJoin methods, where the recent research has shown that such hybrid implementation strategies can execute pattern matching queries more efficiently.
- Cost estimation based on high-order statistics. The cost estimation in our optimization uses high-order statistics (i.e., the frequencies of occurrences of small patterns, also known as motifs, in the data graph) as a basis, providing a more accurate estimate of the cost of the queried pattern. However, it should be noticed that the precomputed statistics are only for the motifs that contains basic types (i.e., the types defined in schema).
- Support for arbitrary type constraints during the optimization process. For graph patterns provided by users, arbitrary type constraints may appear, and in such cases, we cannot directly query statistical information to estimate their costs. Therefore, we propose a new estimation method that considers only the change in the number of matches brought about by expanding one vertex at a time. Thus, we estimate the frequency of a pattern based on its subpatterns’ frequencies iteratively, until the subpattern can be queried from GLogue directly, or it is a single vertex or edge.
Based on the three key techniques, we propose a top-down, cost-based framework for optimizing arbitrary graph pattern matching, aiming to find the optimal execution plan for the arbitrary query patterns.
Case Study
We validated the effectiveness of GOpt through various experiments. Here, we demonstrate the role of GOpt in the entire query optimization process using two real-world cases.
Money Mule Detection. In fraud detection, one of the most common fraud patterns is the money mule pattern, where a fraudster transfers money to a money mule, who then transfers the money to another money mule, and so on, until the money is withdrawn by another fraudster. This can be formulated as a s-t path problem in PatRelQuery: Given two sets of fraudsters $S_1$ and $S_2$ and the hop number $k$, we aim to find all the money transformation paths between the fraudsters in $S_1$ and $S_2$ with the specified hop number. The query written in Cypher is as follows:
MATCH (p1:PERSON)-[p:*$k]-(p2:PERSON)
WHERE p1.id IN $S1 and p2.id IN $S2
RETURN p
Searching for such paths in a large-scale graph is challenging, as it may involve a large number of intermediate results. Two most commonly used approaches is as follows: single-direction expansion, which starts the traversal from vertices in $S_1$, expanding $k$ hops, and then applying a filter to ensure that the end vertices are contained within the set $S_2$; and bidirectional search, which begins traversal from $S_1$ and $S_2$ simultaneously, and when the sub-paths meet in the middle, join them to make result paths. In most cases, the second approach should be more efficient as it can reduce the number of intermediate results.
However, the question is that, is the middle vertex in the path always the best choice for the join? Our case study shows that it is not always true. We have conducted experiments on a real-world graph with $3.6$ billion vertices and $21.8$ billion edges, with the hop number $k$ set to $6$. We obtain five different settings randomly for the source fraudster sets $(S_1,S_2)$ from the real application, each corresponds to different fraudster groups, and the five queries are denoted as $ST_1\ldots ST_5$. For the pattern shown in Figure 5(a), GOpt applies the cost-based optimization to derive the optimal execution plans for $ST_1\ldots ST_5$, as shown in Figure 5(b-d). We notice that for queries with different settings, GOpt may generate different optimal execution plans. This is because the cost model takes into account of the number of intermediate results, which is not only affected by the expanding hops, but also affected by the number of matched vertices in the source fraudster sets.
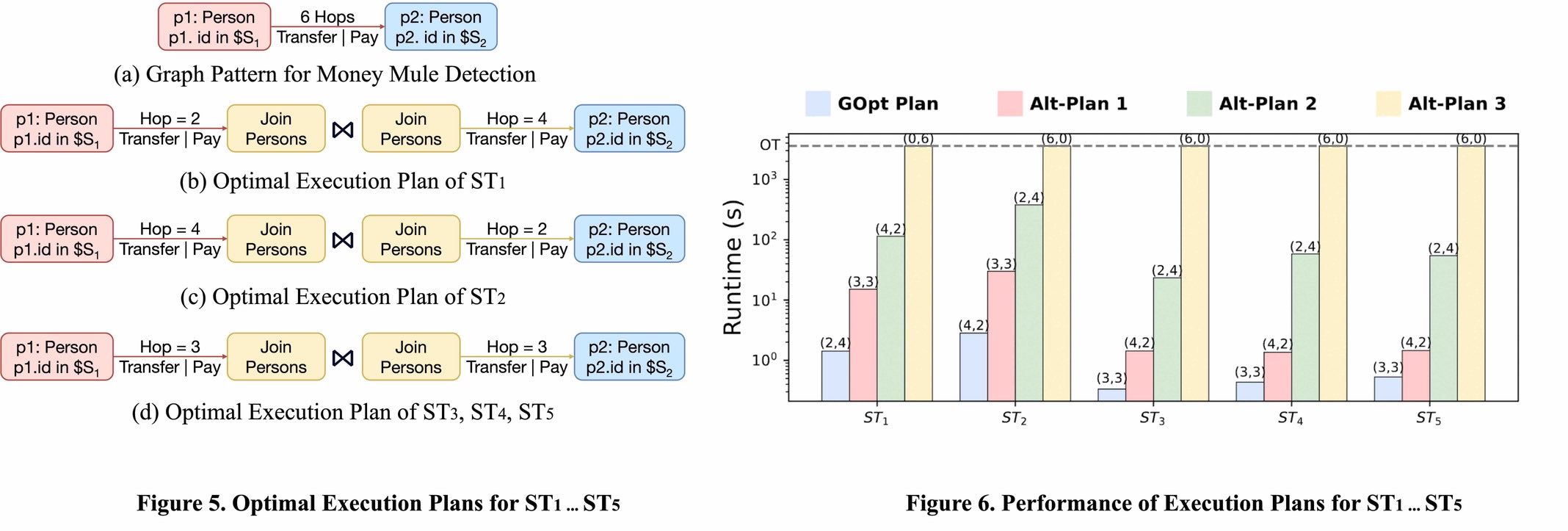 To verify the efficiency, we further generate three alternative plans with different search order for each query as a comparison. The execution time cost of different plans are shown in Figure 6. Here, the tuples above the bars indicate position of the join vertex, e.g., for $ST_1$, the Alt-Plan1 has join vertex in the middle. From the figure, we can see that the plan generated by GOpt outperforms all the alternative plans from $3\times$ to two orders of magnitude, where all the single-direction expansion plans fails to complete the query in 1 hour. Notice that for $ST_1$ and $ST_2$, the plan generated by GOpt outperforms the alternatives that have the join vertex in the middle. This demonstrate the effectiveness of GOpt, that it is able to find the optimal plan adaptively according to the query and the data distribution.
To verify the efficiency, we further generate three alternative plans with different search order for each query as a comparison. The execution time cost of different plans are shown in Figure 6. Here, the tuples above the bars indicate position of the join vertex, e.g., for $ST_1$, the Alt-Plan1 has join vertex in the middle. From the figure, we can see that the plan generated by GOpt outperforms all the alternative plans from $3\times$ to two orders of magnitude, where all the single-direction expansion plans fails to complete the query in 1 hour. Notice that for $ST_1$ and $ST_2$, the plan generated by GOpt outperforms the alternatives that have the join vertex in the middle. This demonstrate the effectiveness of GOpt, that it is able to find the optimal plan adaptively according to the query and the data distribution.
LDBC Interactive Complex Queries. We conducted extensive experiments on the LDBC SNB Interactive Workload to verify the effectiveness of GOpt. Here, we use the IC3 query as an example to compare the execution efficiency of GOpt and Neo4j, with the results shown in the table below.
| Execution Plan | Avg. Runtime(s) | Intermediate Result Num. |
|---|---|---|
| GOpt Optimized Plan | 6.085 | 1,784,536 |
| Neo4j Optimized Plan | 156.845 | 176,547,616 |
The result shows that the execution time of GOpt’s plan is approximately 26 times faster than that of Neo4j’s plan. Additionally, GOpt’s plan produces a mere $1\%$ of the intermediate results generated by Neo4j’s plan, demonstrating a significant reduction in processing overhead. It is evident that, compared to Neo4j, GOpt is able to obtain more efficient execution plans.
Conclusion
This article showcases the optimization framework GOpt in GraphScope, which integrates fragmented graph query optimizations into a unified framework. It offers a cohesive approach to optimizing complex PatRelQueries in real-world applications. For detailed techniques, readers can refer to our original paper. The unified optimization framework GOpt is also gradually being integrated into the main repository of GraphScope, and we welcome interested readers to stay tuned for updates.