Graph Interactive Workloads#
Graph interactive workloads primarily focus on exploring complex graph structures in an interactive manner. There’re two common interactive workloads, namely
Graph traversal: This type of workload involves traversing the graph from a set of source vertices while satisfying the constraints on the vertices and edges that the traversal passes. Graph traversal differs from the analytics workload as it typically accesses a small portion of the graph rather than the whole graph.
Pattern Matching: Given a pattern that is a small graph, graph pattern matching aims to compute all occurrences (or instances) of the pattern in the graph. Pattern matching often involves relational operations to project, order and group the matched instances.
In GraphScope, the Graph Interactive Engine (GIE) has been developed to handle such interactive workloads, which provides widely used query languages, such as Gremlin or Cypher, that allow users to easily express both graph traversal and pattern matching queries. These queries will be executed with massive parallelism in a cluster of machines, providing efficient and scalable solutions to graph interactive workloads.
Tinkerpop and Gremlin#
Apache TinkerPop is an open framework for developing interactive graph applications using the Gremlin query language. We have implemented TinkerPop’s Gremlin Server interface and attempted to support the official traversal steps of Gremlin in GIE. As a result, Gremlin users can easily get started with GIE through the existing TinkerPop ecosystem, including the language wrappers of Python and Gremlin’s console. For language features, we support both the imperative graph traversal and declarative pattern matching in Gremlin for handling the graph traversal and pattern matching workloads in the interactive context, respectively.
Graph Traversal#
In the imperative graph traversal, the execution follows exactly the steps given by the query, where a set of traversers walk a graph step by step according to the corresponding user-provided instructions, and the result of the traversal is the collection of all halted traversers. A traverser is the basic unit of data processed by a Gremlin engine. Each traverser maintains a location that is a reference to the current vertex, edge or property being visited, and (optionally) the path history with application states.
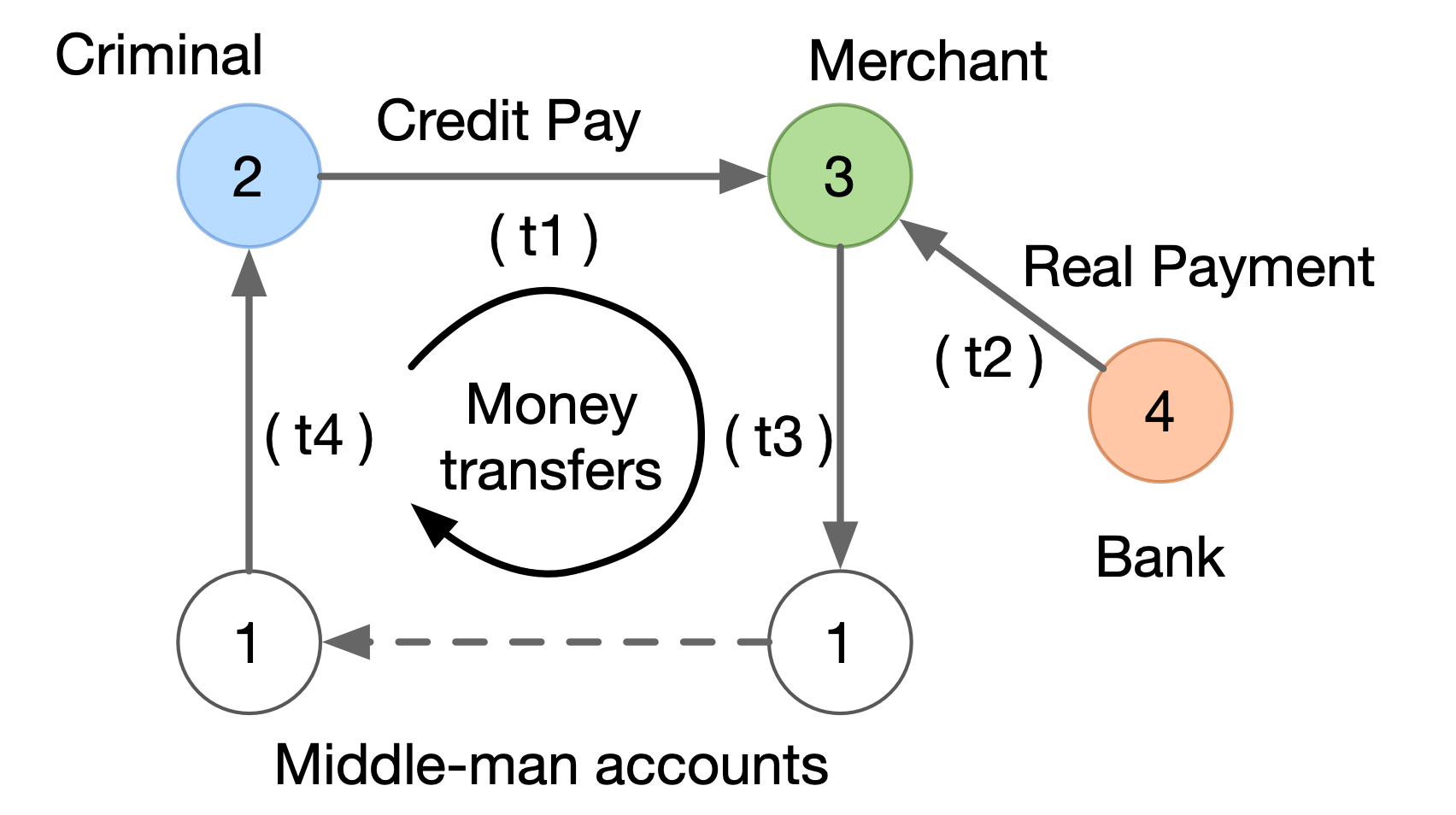
A traversal query for cycle detection.#
The above figure shows a simplified anti-money-laundering scenario via cycle detection.
Below is the corresponding traversal query, which tries to find cyclic paths of length
k starting from a given account.
g.V('account').has('id','2').as('s')
.out('k-1..k', 'transfer')
.with('PATH_OPT', 'SIMPLE')
.endV()
.where(out('transfer').eq('s'))
.limit(1)
First, the source operator V (with the has() filter) returns all the account vertices with an
id of 2. The as() operator is a modulator that does not change the input collection of
traversers but introduces a name (s in this case) for later references. Second, it traverses
the outgoing transfer edges for exact k-1 times using an out() step with a range of lower bound k-1 (included)
and upper bound k (excluded), while skipping any repeated vertices with() the SIMPLE path option.
Such a multi-hop path expansion is a syntactic sugar we
introduce for easily handling the path-related applications.
Third, the where operator checks if the starting vertex s can be reached by one more step, that is,
whether a cycle of length k is formed. Finally, the limit() operator at the end indicates that
only one such result is needed.
Pattern Matching#
Different from the imperative traversal query, the match() step provides a
declarative way of expressing the pattern matching queries. In other words, users only need to describe what the pattern is using match(), and the engine will automatically derive the best-possible execution
plans based on both algorithmic heuristics and cost estimation.
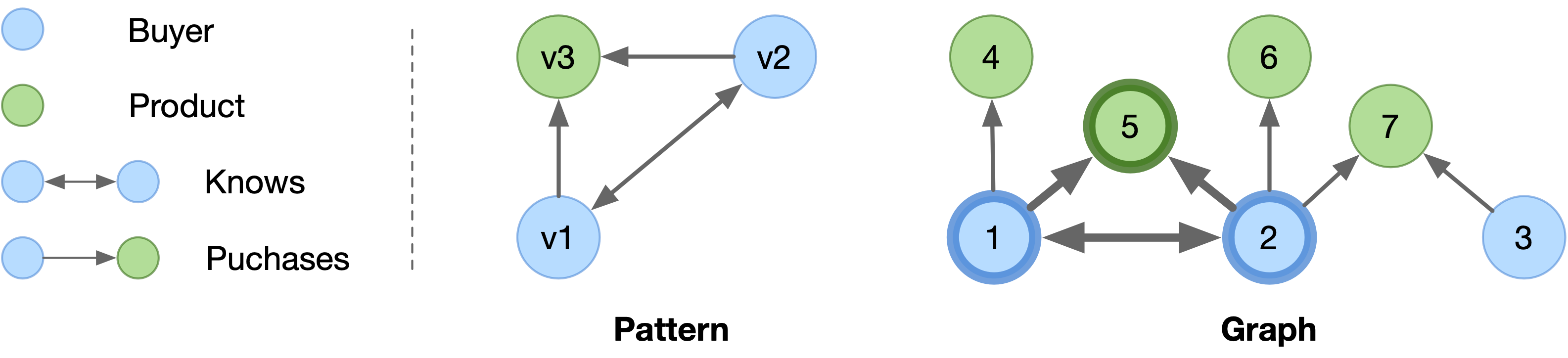
An example of pattern matching.#
The above figure shows an example of pattern matching query, where the pattern is a triangle that describes two buyers who knows each other purchase the same product. In the graph, there is a matched instance highlighted in bolder borders, in which pattern vertices v1, v2 and v3 are matched by vertices 1, 2 and 5, respectively.
g.V().match(
as('v1').both('Knows').as('v2'),
as('v1').out('Purchases').as('v3'),
as('v2').out('Purchases').as('v3'),
)
The pattern matching query is declarative in the sense that users only describes the pattern using the match() step, while the engine determine how to execute the query (i.e. the execution plan) at runtime according to a pre-defined cost model. For example, a worst-case optimal execution plan may first compute the matches of v1 and v2, and then intersect the neighbors of v1 and v2 as the matches of v3.
Neo4j and Cypher#
Neo4j is a popular graph database management system known for its native graph processing capabilities. It provides an efficient and scalable solution for storing, querying, and analyzing graph data. One of the key components of Neo4j is the query language Cypher, which is specifically designed for working with graph data. We have fully embraced the power of Neo4j by implementing essential and impactful operators in Cypher, which enables users to leverage the expressive capabilities of Cypher for querying and manipulating graph data. Additionally, we have integrated Neo4j’s Bolt server into our system, allowing Cypher users to submit their queries using the open SDK. As a result, Cypher users can easily get started with GIE through the existing Neo4j ecosystem, including the language wrappers of Python and Cypher-Shell.
Pattern Matching#
The MATCH operator in Cypher provides a declarative syntax that allows you to express graph patterns in a concise and intuitive manner. The pattern-based approach aligns well with the structure of graph data, making it easier to understand and write queries. This helps both beginners and experienced users to quickly grasp and work with complex graph patterns. Moreover, The MATCH operator allows you to combine multiple patterns, optional patterns, and logical operators to create complex queries, which empowers you to express complex relationships and conditions within a single query. It can be written in Cypher for the above Triangle example:
Match (v1)-[:Knows]-(v2),
(v1)-[:Purchases]->(v3),
(v2)-[:Purchases]->(v3)
Return DISTINCT v1, v2, v3;