Vertex-Centric Model¶
In a single machine environment, developers can easily implement graph analytics algorithms as they have a global view of the graph and can freely iterate through all vertices and edges. When the size of graph data grows beyond the memory capacity of a single machine, graph data must be partitioned to distributed memory, leading to the indivisibility of the whole graph structure.
To allow developers to succinctly express graph analytics algorithms under such environment, the vertex-centric programming model have been developed, with the philosophy of “think like a vertex”. Specifically, a graph analytics algorithm iteratively executes a user-defined program over vertices of a graph. The user-defined vertex program typically takes data from other vertices as input, and the resultant output of a vertex is sent to other vertices. Vertex programs are executed iteratively for a certain number of rounds, or until a convergence condition is satisfied. As opposed to global perspective of the graph, vertex-centric models employ a local, vertex-oriented perspective.
The philosophy of vertex-centric model encourages many programming models, including the Pregel model proposed by Google and the GAS model. These programming models have widely applied in various graph processing systems, such as Giraph, GraphX and PowerGraph.
Pregel Model¶
Pregel was first introduced in a SIGMOD paper published by Google in 2010. A graph analytics algorithm with the Pregel model consists of a sequence of iterations (called supersteps).
“During a superstep the framework invokes a user-defined function for each vertex, conceptually in parallel. The function specifies behavior at a single vertex V and a single superstep S. It can read messages sent to V in superstep S − 1, send messages to other vertices that will be received at superstep S + 1, and modify the state of V and its outgoing edges. Messages are typically sent along outgoing edges, but a message may be sent to any vertex whose identifier is known.”
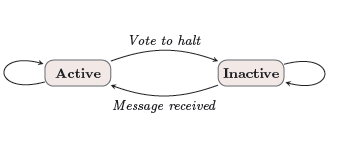
The Pregel model.¶
As shown in the following figure, in each iteration, the state of a vertex becomes inactive if there are no messages sent to it. Once it receives messages, its state will become active again.
The iterations terminate until no messages are sent from any vertex, indicating a halt.
The vertex function can be invoked at each vertex in parallel, since individual vertices communicate via message-passing.
With the Pregel model, the vertex program of single source shortest paths (SSSP) is expressed as follows, where the Compute function is executed for a vertex when it receives messages from other vertices, and sends updates to other vertices after computation.
void Compute(MessageIterator* msgs) {
int mindist = IsSource(vertex_id()) ? 0 : INF;
for (; !msgs->Done(); msgs->Next())
mindist = min(mindist, msgs->Value());
if (mindist < GetValue()) {
*MutableValue() = mindist;
OutEdgeIterator iter = GetOutEdgeIterator();
for (; !iter.Done(); iter.Next())
SendMessageTo(iter.Target(), mindist + iter.GetValue());
}
VoteToHalt();
}
GAS Model¶
However, the performance of Pregel drops dramatically when facing natural graphs which follow a power-law distribution. To solve this problem, PowerGraph proposed the GAS (Gather-Apply-Scatter) programming model for the vertex-cut graph partitioning strategy. The Gather function runs locally on each partition and then one accumulator is sent from each mirror to the master. The master runs the Apply function and then sends the updated vertex data to all mirrors. Finally, the Scatter phase is run in parallel on mirrors to update the data on adjacent edges.
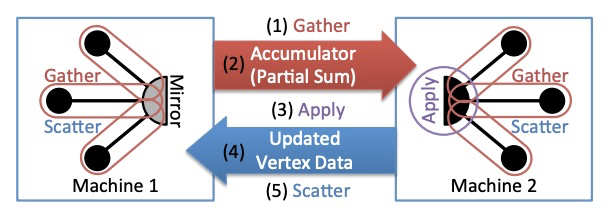
The GAS model.¶
Simulation of Pregel Model in Analytical Engine¶
As we proved in this paper, the analytical engine of GraphScope is able to simulate the vertex centric models. We have implemented the support for Pregel model in the analytical engine, and you can use the Pregel APIs to write your own algorithms. In addition, if you already have your graph applications implemented in Giraph or GraphX, you can run them on GraphScope directly. Better still, the analytical engine can achieve better performance than Giraph and GraphX.
Please refer to related tutorials.