Programming Model: PIE¶
Although the vertex-centric programming model can express various graph analytics algorithms, existing sequential (single-machine) graph algorithms need to be modified to adhere to the “think like a vertex” principle. This makes parallel graph computation a privilege for experienced users only. Additionally, the performance of graph algorithms using the vertex-centric model is sub-optimal in many cases. Each vertex has information about only its 1-hop neighbors, causing information propagation through the graph to be slow and occur one hop at a time. Consequently, it may take multiple computation iterations to propagate a piece of information from a source to a destination.
What is the PIE Model?¶
To address the abovementioned problems, we proposed a new programming model PIE (PEval-IncEval-Assemble) in a SIGMOD paper published in 2017. Unlike the vertex-centric model, the PIE model can automatically parallelize existing sequential graph algorithms with only minor modifications. This makes parallel graph computations accessible to users familiar with conventional graph algorithms taught in college textbooks, eliminating the need to recast existing graph algorithms into a new model.
Specifically, in the PIE model, users only need to provide three functions,
(1) PEval, a sequential (single-machine) function for given a query, computes the answer on a local partition;
(2) IncEval, a sequential incremental function, computes changes to the old output by treating incoming messages as updates; and
(3) Assemble, which collects partial answers, and combines them into a complete answer.
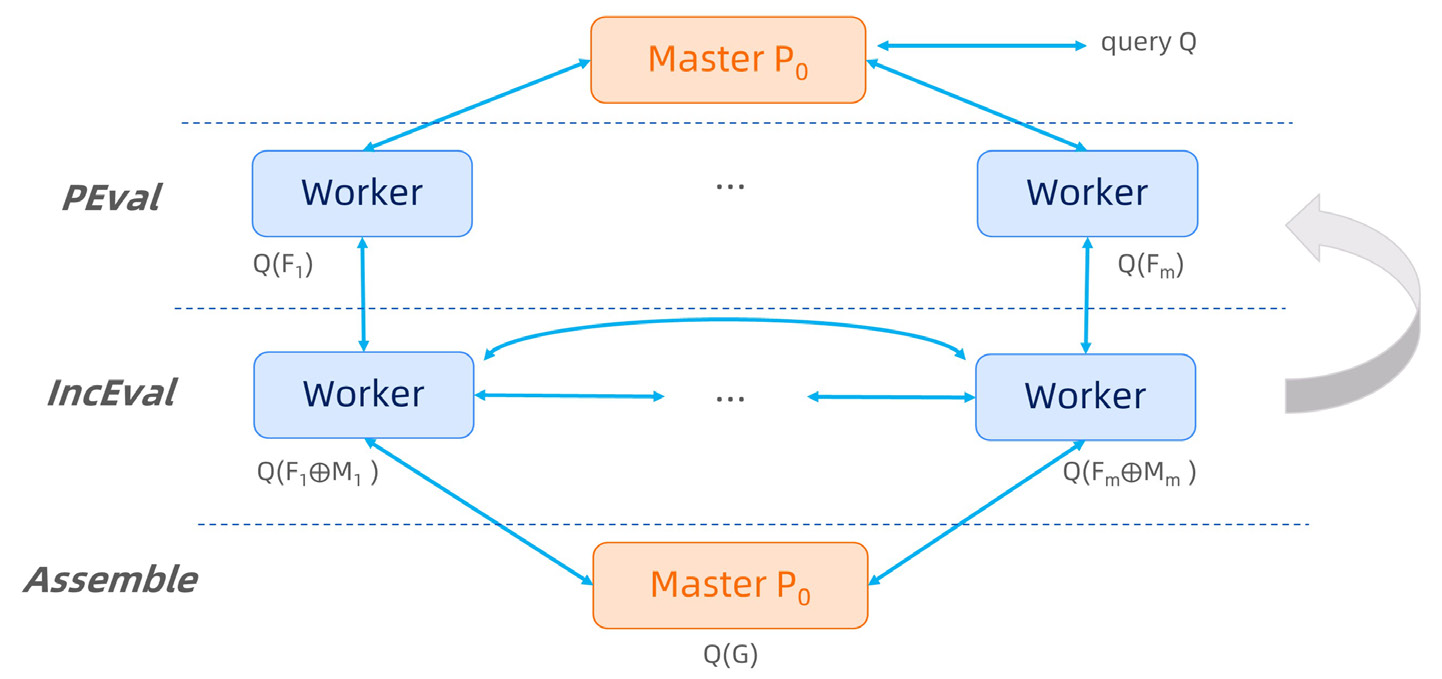
The PIE model.¶
Workflow of PIE¶
The PIE model works on a graph G and each worker maintains a partition of G. Given a query, each worker first executes PEval against its local partition, to compute partial answers in parallel. Then each worker may exchange partial results with other workers via synchronous message passing. Upon receiving messages, each worker incrementally computes IncEval. The incremental step iterates until no further messages can be generated. At this point, Assemble pulls partial answers and assembles the final result. In this way, the PIE model parallelizes existing sequential graph algorithms, without revising their logic and workflow.
In this model, users need not be familiar with the intricacies of processing large graphs in a distributed setting. The PIE model automatically parallelizes graph analytics tasks across a cluster of workers based on a fixpoint computation. Under a monotonic condition, it guarantees convergence with accurate answers as long as the three provided sequential algorithms are correct.
The following code shows how SSSP is expressed with the PIE model in GAE. Note that we only show the major computation logic here.
void PEval(const fragment_t& frag, context_t& ctx,
message_manager_t& messages) {
vertex_t source;
bool native_source = frag.GetInnerVertex(ctx.source_id, source);
if (native_source) {
ctx.partial_result[source] = 0;
auto es = frag.GetOutgoingAdjList(source);
for (auto& e : es) {
vertex_t v = e.get_neighbor();
ctx.partial_result[v] =
std::min(ctx.partial_result[v], static_cast<double>(e.get_data()));
if (frag.IsOuterVertex(v)) {
// put the message to the channel.
messages.Channels()[0].SyncStateOnOuterVertex<fragment_t, double>(
frag, v, ctx.partial_result[v]);
} else {
ctx.next_modified.Insert(v);
}
}
}
}
void IncEval(const fragment_t& frag, context_t& ctx,
message_manager_t& messages) {
auto inner_vertices = frag.InnerVertices();
// parallel process and reduce the received messages
messages.ParallelProcess<fragment_t, double>(
thread_num(), frag, [&ctx](int tid, vertex_t u, double msg) {
if (ctx.partial_result[u] > msg) {
atomic_min(ctx.partial_result[u], msg);
ctx.curr_modified.Insert(u);
}
});
// incremental evaluation.
ForEach(ctx.curr_modified, inner_vertices,
[&frag, &ctx](int tid, vertex_t v) {
double distv = ctx.partial_result[v];
auto es = frag.GetOutgoingAdjList(v);
for (auto& e : es) {
vertex_t u = e.get_neighbor();
double ndistu = distv + e.get_data();
if (ndistu < ctx.partial_result[u]) {
atomic_min(ctx.partial_result[u], ndistu);
ctx.next_modified.Insert(u);
}
}
});
auto outer_vertices = frag.OuterVertices();
ForEach(ctx.next_modified, outer_vertices,
[&channels, &frag, &ctx](int tid, vertex_t v) {
channels[tid].SyncStateOnOuterVertex<fragment_t, double>(
frag, v, ctx.partial_result[v]);
});
}
In the above code, given a source vertex source, in the PEval function, we first execute the Dijkstra’s
algorithm on the sub-graph (fragment) where the source resides to obtain a partial result. After that, the SyncStateOnOuterVertex function is invoked, where the partial result is sent to other fragments to trigger IncEval function.
In the IncEval function, each fragment first receives messages through the message manager, then executes incremental evaluation based on received messages to update the partial result. If the partial result is updated, each fragment needs to execute the SyncStateOnOuterVertex function to synchronize the latest partial result of outer vertices with other fragments to trigger next round of IncEval. Please checkout the following tutorials for more details about how to develop graph applications with the PIE model.